I want to share one of my favorite visual explanations of a somewhat complicated process. As soon as I worked through this myself, I instantly understood what was going on, and it has stuck with me.
What is congestion collapse?
There are billions of devices on the Internet. The Internet is made of a loose confederation of connected networks and each of those has a bunch of devices connected to it; many are well-behaved, some are errant and others evil. Yet the magic of the Internet, the thing that set it apart from all other networks that came before, was that anything on the Internet could usually talk to anything else on the Internet without prior approval. There was no step to reserve bandwidth; no authority to approve or disapprove the connection. There was no telephone network operator that listened to your request, billed you and then connected some wires. You just sent a packet and it probably got there. If it didn’t, maybe you would try again, and it would almost certainly get there this time.
We wrapped the packets in a protocol called TCP (Transmission Control Protocol). It turns packets into conversations: re-sending an occasional lost packet and keeping track of the beginning and end of each session between computers.
This worked great in the very early days. If someone was using more than their fair share of Internet resources, you could probably just call them at their lab and ask them to back off a little. However, in 1986 usage had increased and the Internet had painful episodes of Congestion Collapse: the network was so overutilized that many users experienced severe performance degradation (or complete failure). Even worse than some users being unfairly starved was that sometimes even the packets that were getting through were not useful - they were stale packets, or repeats of packets that had already gotten through a hundred times (but TCP couldn’t tell, so it just kept sending the same duplicates)1.
Some heros of the early Internet like Van Jacobson, Sally Floyd, Vern Paxson and others built algorithms to prevent congestion collapse. New algorithms and tweaks to existing ones continue; this remains an area of active research 35 years later. However, there’s a property of all good congestion avoidance algorithms: they do Additive Increase and Multiplicative Decrease2.
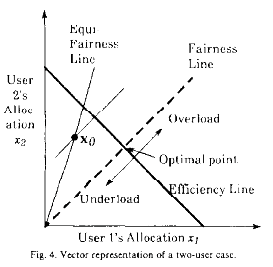
I learned why this is a fundamental truth from a beautiful paper by Dah-Ming Chiu and Raj Jain called Analysis of the Increase and Decrease Algorithms for Congestion Avoidance in Computer Networks. Here’s the important drawing (pg. 6):
To explain it, we have to define the problem and goals; Jain and his students did this in this paper and several others. My shortened version:
There’s a network with many users and many links; for simplicity we’re going to assume the users want to use more capacity than the links have.
Each user needs to choose an amount of capacity to use (the offered load). They can adjust this over time.
Their choice should provide fairness: Every user gets an equal division of the capacity.
Their choice should provide efficiency: The total offered load is equal to the total capacity. We don’t want to waste network bandwidth.
There is no central resource manager, no reservation system, no communication between the users. Users don’t even know how many other users there are, and they can’t see other traffic.
What do the users get? Well, they get to know if their traffic is getting through. That’s about it. For the Chiu/Jain model, we’re going to make some simplifying assumptions.
Think of the challenge like a card game, played in a series of rounds. For each round, every user has to choose an offered load without consulting any other players. This is how much traffic they’ll send this round.
If the total of the offered loads of all players is less than the capacity, then 100% of everyone’s traffic gets through.
If the total of the offered loads exceeds the capacity, then everyone observes at least one dropped packet.
That’s it. Users just play rounds over and over again. Chiu and Jain demonstrated that a certain class of algorithms called Additive Increase/Multiplicative Decrease (AI/MD) will converge to a broad state of fairness and efficiency.
Comparing Strategies
AI/MD refers to the strategy that the players will follow during the game:
When all traffic gets through, we must be under capacity. We will each add to our offered load.
When we see a loss, we must be over capacity. We will all decrease our offered load multiplicatively (we’ll multiply by a number less than 1, like \(\frac{1}{2}\)).
It’s probably not intuitive to you why this leads to stability, but if you step through the drawing, it makes sense very quickly. I whipped up a little simulation based on the drawing to make it even easier. Pick a behavior type and then click “Step” repeatedly to see how/if the users converge. You can pick a different starting point by clicking anywhere.
| Strategy | No Loss in Round (under capacity) | Loss in Round (over capacity) |
|---|---|---|
| \(load := load + C\) | \(load := load - C\) | |
| \(load := load + C\) | \(load := load \cdot \dfrac{1}{N}\) | |
| \(load := load \cdot N\) | \(load := load - C\) | |
| \(load := load \cdot N\) | \(load := load \cdot \dfrac{1}{N}\) |
Each point is the offered load for one round. User 1’s offered load is the x-coordinate, and user 2 is the y-coordinate. If the sum of these two loads is over the efficiency line, it exceeds the capacity (in this simulation, the capacity is “5” of whatever units you like :-) ).
If the load is under the capacity, then all the packets get through, no loss, so we follow the increase rules for the next round.
If the load exceeds the capacity, then all the packets can’t possibly get through, and we experience loss, so we follow the decrease rules for the next round.
The grey lines are the projection lines for the strategy. If you click a few different strategies, you can see that any multiplicative increase or decrease is a projection either towards or away from the origin \((0,0)\). Any additive increase or decrease is a line with a slope of 1.
As you step through, if you use AI/MD, you will see that you inevitably move to the line of maximum fairness, and then oscillate around the line of maximum efficiency. Every now and then, you go over-capacity, have a loss, and drop back down. Then you work your way up. But the allocation remains fair.
Not so for the other strategies. Some never find fairness but at least don’t get worse. Some become totally unfair, eventually punishing one user.
Reality
You may feel like we made strong simplifying assumptions when making this model, and you’d be right. Some practical notes:
What’s with the oscillation around the optimum point?
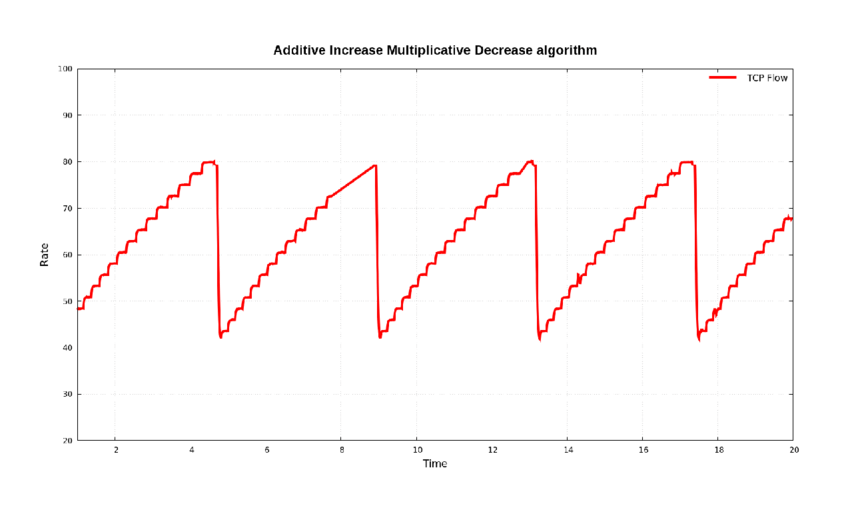
You may have noticed that in AI/MD, once we reach fairness, we oscillate around the efficiency line. We slowly creep up to optimum, go slightly over, bounce back down and then start slowly creeping up again.
This is actually an observed behavior of many earlier TCP implementations! It’s called “sawtoothing” because if you plot the bandwidth for one user over time, it looks like the teeth on a saw blade3:
Modern TCP implementations choose the increase differently. For instance, BIC and CUBIC do a binary search to find the optimal bandwidth; they try to halve the distance between current bandwidth and “last max I saw” during each additive step. This is asymptotically equivalent to additive increase, so it theoretically fits the Jain model while practically getting to the max point much more quickly.
(CUBIC may be what you’re using right now to look at this web page; it is the default for many OSes’ TCP as well as common QUIC implementations.)
These “rounds” are nothing like reality!
We unfairly divided time into a bunch of rounds in our capacity allocation game. In reality, there’s no synchronized concept of rounds, just a bunch of systems acting independently. This is a fair criticism but it turns out to not matter much for the coarse-grained stability of the system.
However, we do observe that round trip times (RTTs) do affect bandwidth sharing. If user 1 has a much longer RTT to the server than user 2, then user 1 may end up with an unfairly small share of the bandwidth. You can think of this as user 1’s “round” is much slower than user 2, so it takes much longer for user 1 to add bandwidth.
This is an area of research called LFNs (“Long Fat Networks” or sometimes “Elephant Networks”). This is common for satellite links, especially non-LEO. There are algorithm adjustments that try to compensate.
Lots of things cause packet loss, not just congestion!
Fewer than you might think. The physical bit error rate for an ethernet link is usually \({10}^{-12}\) or better, meaning that fewer than 1 out of every trillion bits gets corrupted. Ethernet (and other links) typically have a corruption detection and retry algorithm that will try to resend a corrupted packet once before giving up, making the observed bit error rate due to random noise corruption extremely low. Similar story for backbone links like fiber. Adding up all the BERs over the links on a path still results in small numbers.
However, there are other important sources of loss. One of the big ones is a bursty loss: a burst of packet loss over a short interval. This can happen with wifi, cellular networks and other networks with wireless links. In our simulation, that might appear as multiple rounds in a row of loss, and repeated multiplicative decrease. To your application, it looks like a complete stall, followed by a recovery period to get back to steady state.
One strategy here is to limit the rate at which you’ll apply multiplicative decreases (based on the assumption that if you see loss in multiple rounds, it’s a bad connection, not congestion). As well, things like CUBIC and Slow Start that can rapidly try to add back towards an old max (before the bursty loss). Many wireless links try hard to hide bursty losses from TCP by retransmitting packets after the loss is over, while adjusting power, bandwidth, coding and other things. Finally, there’s a class of algorithms (FAST TCP and CERL+) that use changes in the RTT to detect oncoming congestion.
However, these approaches still have to behave like AI/MD (at least at a coarse granularity) to play nicely with all the other Internet users (this is called TCP Fairness: no matter how fancy your new algorithm is, it can’t break the internet for everybody else).
Is this only for computers?
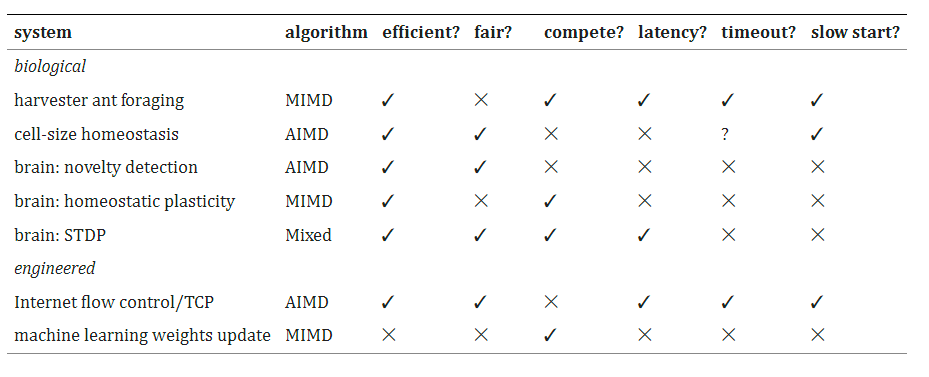
Apparently not. In A feedback control principle common to several biological and engineered systems, Suen et. al. find several biological systems that use AI/MD for feedback control. Here’s a table from their paper:
Congestion Collapse. CSE461 at University of Washington. https://courses.cs.washington.edu/courses/cse461/17au/ ↩
Some modern algorithms do not simply follow AIMD; they may have very different schemes for adjusting offered load. But at the end of the day, when they see congestion loss, they must decrease multiplicatively. ↩
Talpur, Ali. (2017). Congestion Detection in Software Defined Networks using Machine Learning of Ali Murad Talpur. 10.13140/RG.2.2.14985.85600. ↩