This is a brief tour of a programming language called Prolog, built around a “Knights and Knaves” problem. This is a logic puzzle where you’re on an island with 8 animals; each animal is either a liar or a truth-teller, and you have to decide which animals you can trust.

If you’ve never used Prolog before, hopefully this gives you the flavor of logic/query programming in about as much time as it takes to drink a cup of coffee.

Knights and Knaves?

Knights and Knaves are a class of logic puzzles where there’s a set of characters, and each character is either a:

Knight: always tells the truth
Knave: always lies

The characters will give you statements and you have to decide whether each one is a Knight or a Knave. You do this by examining the logical consistency of what they’re saying.

The king of Knights and Knaves problems (and many other puzzles) was a mathematician named Raymond Smullyan. Here’s a simple example from his book:

You arrive on an island with 2 people, A and B. A says: “At least one of us is a Knave.”

We must decide if A is a Knight or Knave, and also decide if B is a Knight or Knave.

In this example, it’s easy enough to try some alternatives and see where they lead:

Suppose A is a Knave: Then the proposition “At least one of us is a Knave” is true (because A is a Knave). But then A isn’t lying, A is telling the truth. Knaves always lie, so this is a contradiction.

OK, let’s try the other way.

Suppose A is a Knight: Then the proposition “At least one of us is a Knave” is true (because A is a Knight and always tells the truth). Then, B must be a Knave (because otherwise, there will be 0 Knaves, and the proposition won’t be true).

The assignment A is a Knight, B is a Knave satisfies all the constraints of the problem. And, in this case, it is the only assignment that satisfies. This is the structure of all Knights and Knaves problems. We’re trying to find an assignment (Knight or Knave for each character) that satisfies our set of constraints that we’ll derive from the character statements.

The bigger problem

We’ll solve a larger “Knights and Knaves” problem with Prolog. I encountered this one when I did a team-building “Zoom escape room” (though we didn’t use Prolog to solve it).

Horse: Neigh, I wouldn’t lie, but the cow would.
Chicken: The silly goat talks too much, but at least he’s honest.
Cow: Obviously, you can’t trust the tricky cat.
Sheep: One of my hooved brethren is a liar.
Pig: The horse is supremely trustworthy.
Goose: I’m the only honest bird.
Goat: There are 6 four-legged creatures. The number of lying four-legged creatures is equal to the number of lying birds.
Cat: There are as many total liars as there are birds, but I’m not one of them.
Problem Statement: Who are the two liars?

So we have our characters, and our statements. We also have an extra constraint - there are exactly two lying animals (Knaves).

We need to find an assignment of Knights and Knaves to these 8 animals such that 2 are Knaves (and their statements are lies), and 6 are Knights (and their statements are true).

If you wanted to solve this by guessing an assignment, and then checking the statements to see if it works, you would require \(\binom{8}{2} = 28\) assignments to exhaustively search.

Let’s try using a computer instead!

Prolog

Prolog is a Logic Programming Language and a Query Language.

These are much different than imperative languages like C, Go or Python where your program is mostly a series of instructions and operations to perform, with things like conditionals (if/else) to adjust the flow/order that is followed, and functions or classes to organize these instructions.

You might be familiar with a very popular query language: the Structured Query Language (SQL). We use SQL to select items from a database that satisfy our conditions.

However, in Prolog, we’re not going to query a database that has rows of records or transactions or something like that. We’re going to query a set of Facts and Rules that we introduce into our logical universe “database.”

Here are some example facts:

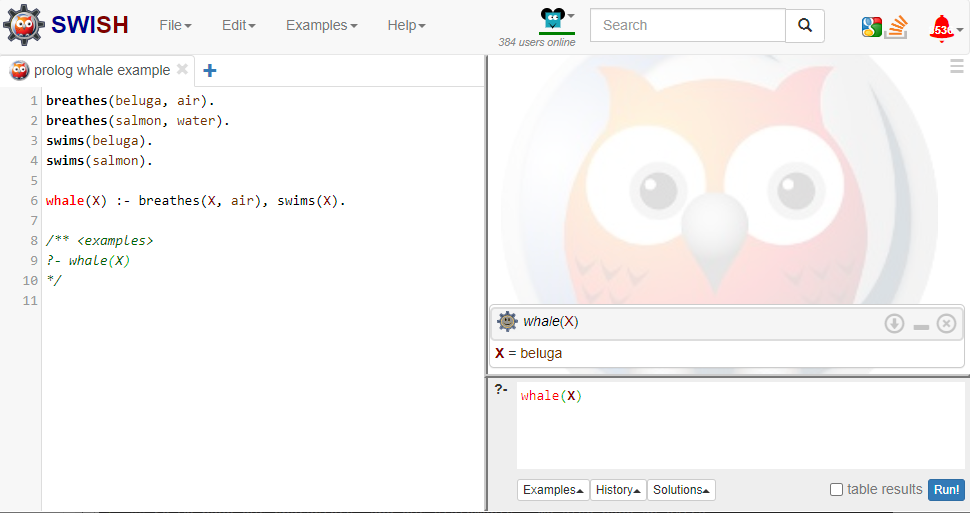
breathes(beluga, air).
breathes(salmon, water).
swims(beluga).
swims(salmon).

and here is an example rule:

whale(X) :-
  breathes(X, air),
  swims(X).

This rule says that an \(X\) satisfies \(whale\) if it breathes air and swims. The :- introduces a new rule (Horn clause). The body of the rule is a set of predicates or goals. A comma , is used to conjoin goals (logical AND), and a semicolon ; is used to disjoin goals (logical OR).

Finally, once you have your facts and rules loaded, you run one or more Queries. Ours will be simple: tell me a whale:

?- whale(X)

You can try this out right now in SWISH, the online Prolog environment. Click “Run” and you’ll see that it tells you “beluga”.

Constraint Logic Programming (CLP)

The above pure Prolog is technically enough to solve our problem, but there’s a lot left to figure out. We’re going to use a very helpful library that will work with the animal’s logical statements, called Constraint Logic Programming. Specifically, we are going to have each animal be a variable in our program. The variable will be Boolean: it will be either True (if the animal is a Knight, or truth-teller) or False (for Knaves/liars). This means we will use CLP(B), the version of CLP for boolean variables.

If we find an assignment of True or False to all eight animal variables that satisfies all the constraints, then we’ve solved the problem.

CLP(B) lets you make Boolean statements according to these rules:

0               false
1               true
variable        unknown truth value
atom            universally quantified variable
~ Expr          logical NOT
Expr + Expr     logical OR
Expr * Expr     logical AND
Expr # Expr     exclusive OR
Var ^ Expr      existential quantification
Expr =:= Expr   equality
Expr =\= Expr   disequality (same as #)
Expr =< Expr    less or equal (implication)
Expr >= Expr    greater or equal
Expr < Expr     less than
Expr > Expr     greater than
card(Is,Exprs)  cardinality constraint
+(Exprs)        n-fold disjunction
*(Exprs)        n-fold conjunction

We’re actually only going to use a few of these. In addition, we’re going to use these predicates as glue between our logical statements and the program we want Prolog to run:

sat(Expr): Contribute a constraint to the program (tell Prolog it must satisfy Expr).
labeling([A, B, C]): Emit all values that satisfy (otherwise it just emits the minimized form of the constraints).

Basic Skeleton

Here’s our basic Prolog with CLP(B) program skeleton:

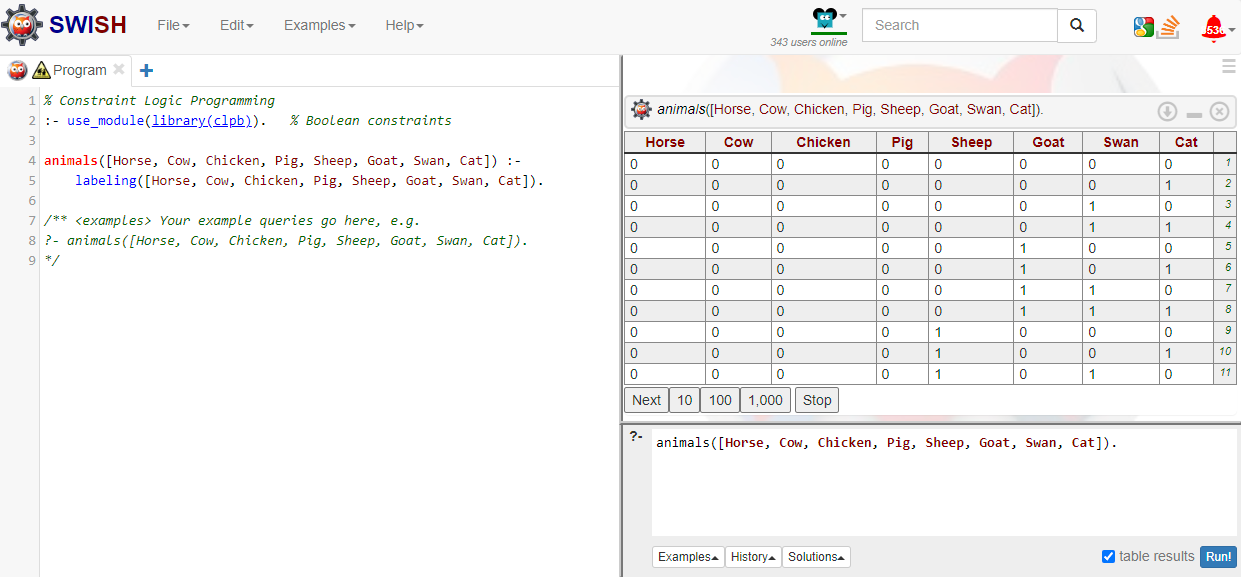
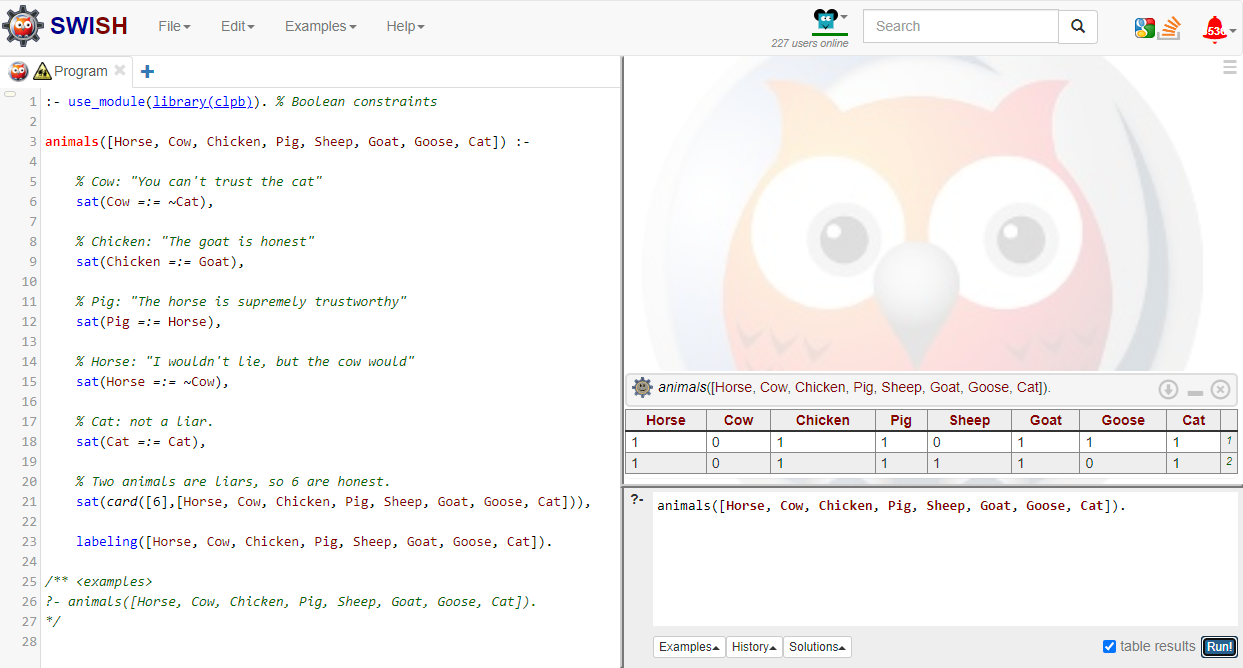
:- use_module(library(clpb)).

animals([Horse, Cow, Chicken, Pig, Sheep, Goat, Goose, Cat]) :-
  labeling([Horse, Cow, Chicken, Pig, Sheep, Goat, Goose, Cat])

?- animals([Horse, Cow, Chicken, Pig, Sheep, Goat, Goose, Cat])

If you run it on SWISH (I recommend checking the “table results” button), you’ll get a labeling of the variables that satisfies our constraints. Wait, what constraints? Oh yeah, we didn’t specify any, aside from that the variables have to be binary and there are 8 of them (one for each animal). So Prolog will happily output one such labeling (namely, “all False”). And it has some buttons “Next”, “10” and so on. You can click those to get more labelings. All the way up to \(2^8=256\) labelings, all the possible ways each animal could be assigned true or false.

Not very interesting. Time to add some constraints.

Our first constraint: Cow says the cat is a liar

Let’s pick the Cow as our first animal.

Obviously, you can’t trust the tricky cat.
– The Cow

He’s telling us that the cat is a liar. You may be tempted to make our first constraint “Cat is a knave/liar”, which we would represent like this:

sat(~Cat)

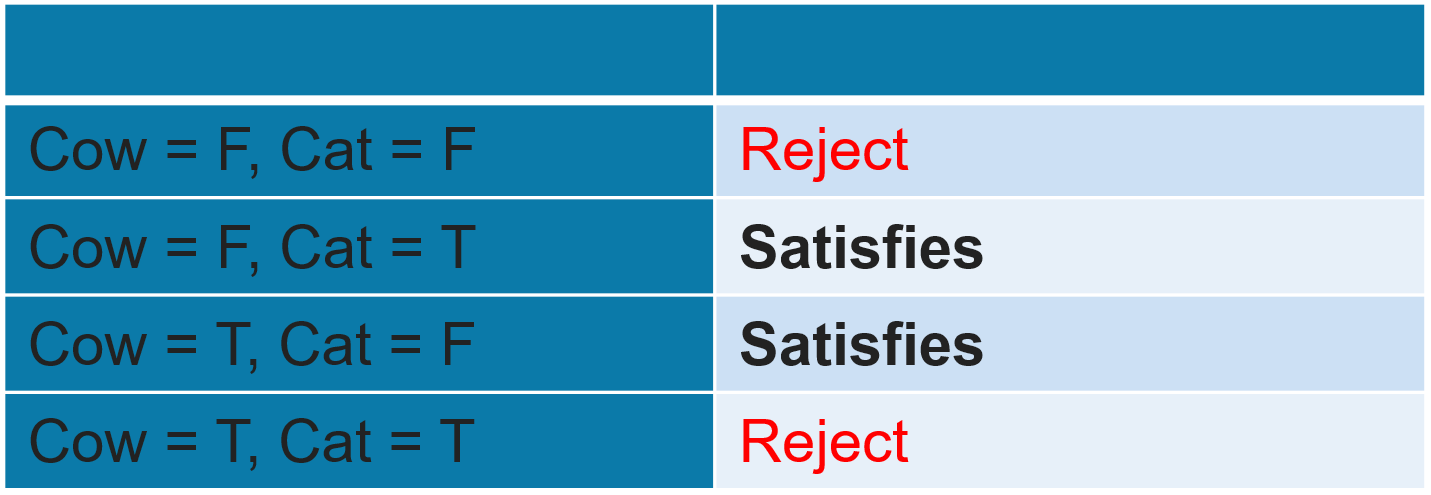
This says, “The solution must satisfy this condition: Cat is false” (knave). However, that’s not right. The cow could be lying (in which case the cat is necessarily a knight/truth-teller).

The true condition is that either:

The cow is telling the truth, and the cat is a knave/liar, or
The cow is lying, and the cat is a knight/truth-teller.

or, this truth-table:

We’ll use the equality operator =:= to encode this. The value (true or false, knight or knave) of the expression Cow is equal to the value of the expression ~Cat:

% The cow says the cat is a liar.
sat(Cow =:= ~Cat)

This will be the form of all of our constraints: sat(Animal =:= WhatTheySaid). If they are a truth-teller, then their statement is true.

If you add this constraint to the Prolog program and run it, you’ll see that you now get 128 results instead of 256, and in each of the results, Cow and Cat have different values - either the Cow is true and the Cat false (liar), or vice-versa.

:- use_module(library(clpb)). % Boolean constraints

animals([Horse, Cow, Chicken, Pig, Sheep, Goat, Goose, Cat]) :-
    % The cow says the cat is a liar.
    sat(Cow =:= ~Cat),
    
    labeling([Horse, Cow, Chicken, Pig, Sheep, Goat, Goose, Cat]).

?- animals([Horse, Cow, Chicken, Pig, Sheep, Goat, Goose, Cat]).

Three More Animals

Let’s add constraints for 3 more animals - the pig, chicken and horse.

These are pretty straightforward to encode following the work we did for the cow:

% Pig says "The horse is supremely trustworthy."
sat(Pig =:= Horse),

% Chicken says "The silly goat talks too much, but at least he's honest."
sat(Chicken =:= Goat),

% Horse says "Neigh, I wouldn't lie, but the cow would."
sat(Horse =:= ~Cow),

Once we add these constraints, you can see that there are only 16 labelings that satisfy. Each of our constraints reduced the solution space by half.

Add the Cat

There are as many total liars as there are birds, but I’m not one of them.
– The Cat

This is a statement that allows at least two interpretations. Let’s break it into two expressions:

Expression 1: “There are as many total liars as there are birds”

Expression 2: “I am not a liar”

First, note that Expression 1 is plainly true. The problem statement says there are two liars, and there are two birds in the drawing.

What do we do with Expression 2? There are two interpretations.

Useless aside: In this interpretation, the first part of the statement is viewed as just filler. There are obviously two birds, and the problem statement says there are two liars. If the second expression is true, then the whole statement is true. If the second expression is false, then the whole statement is false overall. This is the case for any true expression “logically ANDed” with any other expression. Thanks, cat, but Expression 1 is not helpful.
True Implication: In this interpretation, the two halves of the statement must both be true or both be false. If you’re a knave, it’s not just that your overall statement is a lie; every single expression therein is a lie.

If you use the True Implication interpretation, then the cat has proven it is a truth-teller in its own statement. From this you can trivially tell the truthfulness of the Cow, and then the Horse and Pig. That’s not very much fun, and assumes something about the nature of being a Knave that I don’t think is fair. I’m going to use the useless aside interpretation.

OK, let’s encode the statement. We’ll leave out Expression 1, because it’s plainly true, and True AND X is always X. Expression 2 is just the cat asserting it isn’t a liar:

% Cat says "I am not a liar"
sat(Cat =:= Cat),

If you add this constraint and run it, you will still see exactly 16 results. This is because we’ve added a useless constraint. Every animal would say it isn’t a liar. This is called a tautology. Doesn’t hurt, but doesn’t help.

(If you’d like, try adding the constraint according to the True Implication interpretation. That means we are certain the cat is a truth-teller, so just add sat(Cat),)

There are Two Liars

Now let’s code the problem statement.

Who are the two liars?

It has helpfully told us there are exactly two liars (two variables are false, and six are true). To do this, we’ll use the cardinality constraint:

The Boolean expression card(Is,Exprs) is true iff the number of true expressions in the list Exprs is a member of the list Is of integers and integer ranges of the form From-To. For example, to state that precisely two of the three variables X, Y and Z are true, you can use sat(card([2],[X,Y,Z])).

2 liars means that 6 of the animals are truth-tellers/knights. In our system, truth teller variables have the value true (or 1). So:

sat(card([6],[Horse, Cow, Chicken, Pig, Sheep, Goat, Goose, Cat])),

Note that there’s no equality =:= in this statement, because no possibly-lying animal said it. We know this statement to be true, it must be satisfied. Our full program now looks like:

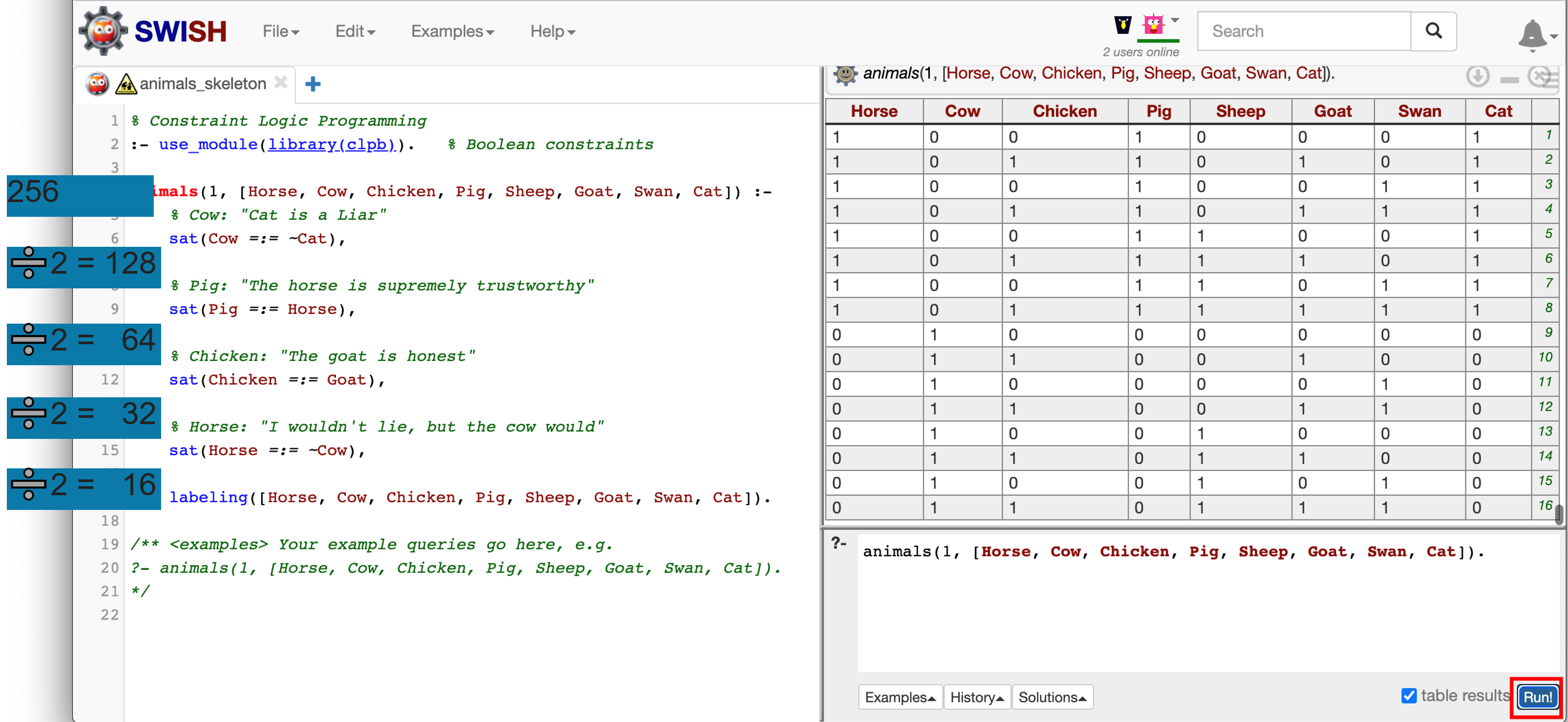
:- use_module(library(clpb)). % Boolean constraints

animals([Horse, Cow, Chicken, Pig, Sheep, Goat, Goose, Cat]) :-
    
    % Cow: "You can't trust the cat"
    sat(Cow =:= ~Cat),
    
    % Chicken: "The goat is honest"
    sat(Chicken =:= Goat),
    
    % Pig: "The horse is supremely trustworthy"
    sat(Pig =:= Horse),
    
    % Horse: "I wouldn't lie, but the cow would"
    sat(Horse =:= ~Cow),
    
    % Cat: not a liar.
    sat(Cat =:= Cat),

    % Two animals are liars, so 6 are honest.
    sat(card([6],[Horse, Cow, Chicken, Pig, Sheep, Goat, Goose, Cat])),
    
    labeling([Horse, Cow, Chicken, Pig, Sheep, Goat, Goose, Cat]).

/** <examples> 
?- animals([Horse, Cow, Chicken, Pig, Sheep, Goat, Goose, Cat]).
*/

If you run this in SWISH, you’ll see that we went from 16 down to 2 possible labelings. Almost there.

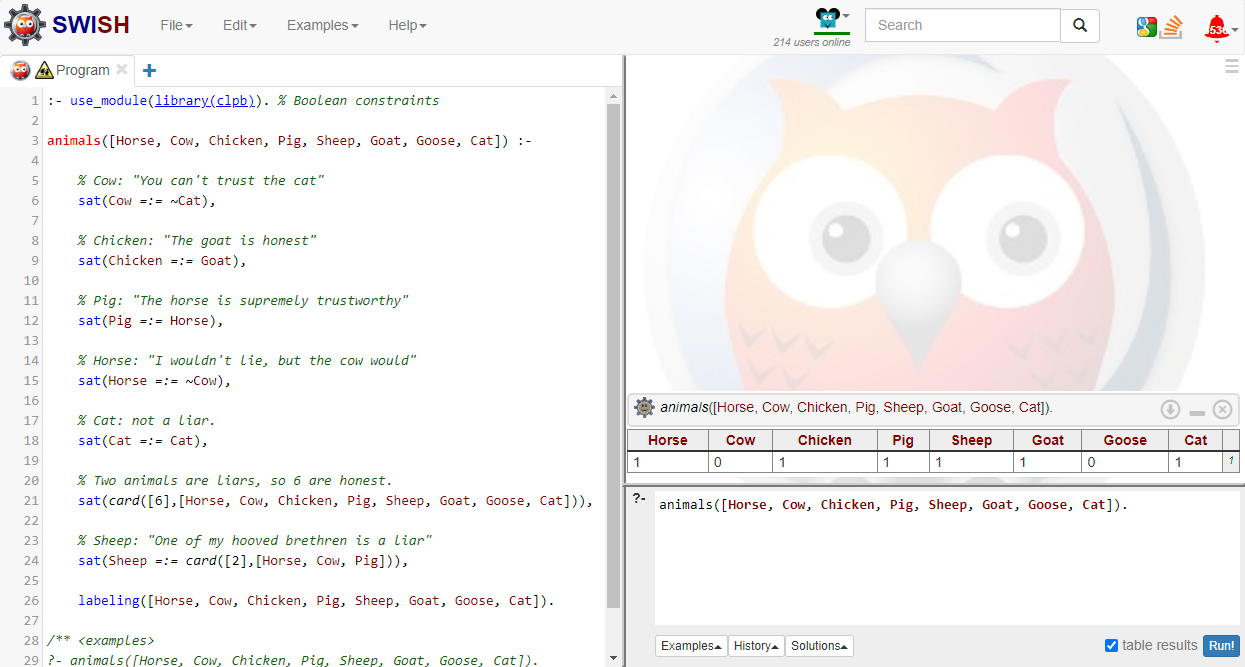
Liars with Hooves

One of my hooved brethren is a liar.
– The Sheep

This one is a combo of cardinality and equality. The sheep says one of the other hooved animals is a liar, but it’s possible they are all honest and the sheep is the liar.

% Sheep: "One of my hooved brethren is a liar"
sat(Sheep =:= card([2], [Horse, Cow, Pig])),

Here’s the entire program so far:

:- use_module(library(clpb)). % Boolean constraints

animals([Horse, Cow, Chicken, Pig, Sheep, Goat, Goose, Cat]) :-

    % Cow: "You can't trust the cat"
    sat(Cow =:= ~Cat),

    % Chicken: "The goat is honest"
    sat(Chicken =:= Goat),

    % Pig: "The horse is supremely trustworthy"
    sat(Pig =:= Horse),

    % Horse: "I wouldn't lie, but the cow would"
    sat(Horse =:= ~Cow),

    % Cat: not a liar.
    sat(Cat =:= Cat),

    % Two animals are liars, so 6 are honest.
    sat(card([6],[Horse, Cow, Chicken, Pig, Sheep, Goat, Goose, Cat])),
    
    % Sheep: "One of my hooved brethren is a liar"
    sat(Sheep =:= card([2],[Horse, Cow, Pig])),

    labeling([Horse, Cow, Chicken, Pig, Sheep, Goat, Goose, Cat]).

/** <examples>
?- animals([Horse, Cow, Chicken, Pig, Sheep, Goat, Goose, Cat]).
*/

If you run this, you’ll get back exactly one result. We’ve found the solution, with Prolog’s help. The Cow and the Goose are liars!

Epilogue: Leftover constraints

We did find the solution. But we still have constraints leftover from the Goat and the Goose that we didn’t code. It turns out we didn’t need all the constraints to solve the problem.

However, hopefully our solution is consistent with all the constraints. You saw how when we added constraints, we saw the number of results shrink. If we add more constraints from the problem, will it shrink further (to 0)?

We can code the statements from the Goose and Goat like this:

% Goose: "I'm the only honest bird"
sat(Goose =:= ~Chicken),

% Goat: "The number of lying four-legged creatures is equal
% to the number of lying birds"
sat(Goat =:=
  card([2],[Chicken, Goose])*card([6],[Horse,Cow,Pig,Sheep,Goat,Cat]) +
  card([1],[Chicken, Goose])*card([5],[Horse,Cow,Pig,Sheep,Goat,Cat]) +
  card([0],[Chicken, Goose])*card([4],[Horse,Cow,Pig,Sheep,Goat,Cat])
)),

If you add them to the program, you will find that there is still exactly one solution (and that it’s the same).

This demonstrates a principle of our logic program, it can be:

Under constrained: Many solutions. We don’t have enough constraints to narrow it down (and prolog can keep giving us more solutions until it runs out).
Perfectly constrained: Exactly one solution, the goal for Knights and Knaves puzzles.
Over constrained: Zero solutions. The constraints contain a contradiction, and there is no possible set of boolean values that satisfies all constraints. If we end up here with Knights and Knaves, we should suspect a bug in our program or invalid problem statement.

Extra Credit

We used 6 animal statements and the problem statement, so 7 total constraints. I picked them in an order to suit my blog. What’s the minimum number of constraints, if you choose different orderings?
Do you need the problem statement (“there are two liars”)?
Two-term Boolean constraints (Cow =:= ~Cat) either reduce the space by a factor of 2, or do nothing (if they’re tautological). What about the cardinality constraints? (Try putting sat(card([6],[Horse, Cow, Chicken, Pig, Sheep, Goat, Swan, Cat])), as the first constraint.
Try removing labeling(), and then commenting out a few constraints. You return to constraint propagation mode; Prolog will try to minimize your constraints.
Instead of coding “hooved brethren” as [Horse, Cow, Pig], you could code them as facts (feet(Horse, Hooves)).
An example of a similar problem written in pure Prolog (no CLP(B)) is here.

Outro: Why?

There are lots of cool things you can do with Prolog and CLP(B), like:

You can find this and other examples at https://github.com/triska/clpb.

As well, query languages pop up from time to time in other places. Policy is a great example because when you do a policy check, you are essentially querying a set of rules/constraints to see if they allow or deny some action or document or whatever. The Open Policy Agent uses a language called Rego, which is inspired by Datalog (which in turn, is a subset of Prolog).

This blog didn’t cover it, but if you express constraints in logic programs then you have opportunity for some powerful operations:

You can optimize on the logic directly; you could elide tautological constraints, for example.
You can detect over-constrained systems: a firewall could tell you “there is no request that could pass through these rules”.
You can detect tautological constraints: a firewall could say “this rule has no effect”.
You can transparently locate different parts of a policy evaluation in different parts of your system (for instance, one policy program could be compiled so that low-level portions are checked in an FPGA or ASIC, and higher-level portions are checked in a CPU, but the combined system behaved as if it was just one centralized policy). This is hard to do safely/automatically outside of a logic program because of the risk of introducing “holes” in complex policies. (I think this is possible but I haven’t seen it)

In logic programming, the constraints are still primitive, represented directly in the program. In our example, we never told Prolog how to find the animals, we just told it what a valid solution would look like.

You can compare this to imperative models where the logic has been converted by the programmer into operations to perform in order. eBPF is an example of this: even when it is used for policy, it’s an imperative program (machine code for a virtual machine). It’s difficult to go from a BPF program back to the logical constraints that caused it to be written, so “finding solutions” to a BPF filter is hard. However, it is very easy to evaluate whether a particular input is accepted by the filter: just run the program.

I am more comfortable writing imperative programs rather than logic programs, but I thought it was fun to explore something different. I hope if you’ve never played with Prolog before, you had fun too.

Prolog and Lying Animals